应用统计学与R语言实现学习笔记（十四）——案例与实践

Chapter 14 Case and Practice

本篇是第十四章，内容是案例与实践。这里其实是对我公选课的作业做了个汇总。

1 描述性统计与抽样分布

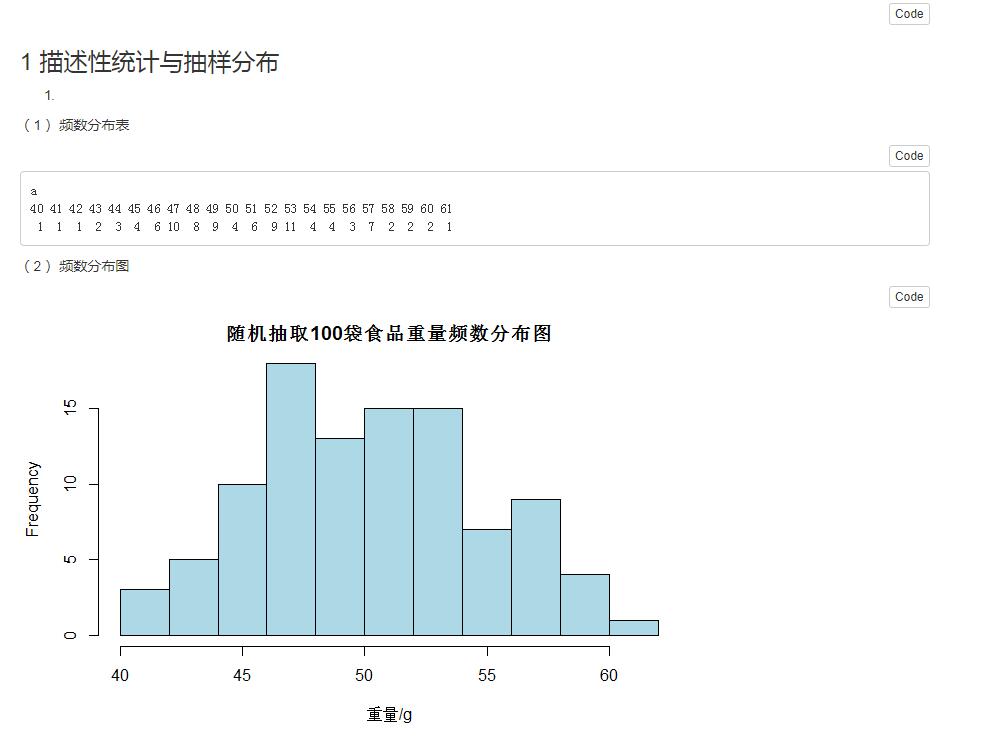
1.一种袋装食品用生产线自动装填，每袋重量大约为50g，但由于某些原因，每袋重量不会恰好是50g。下面是随机抽取的100袋食品，测得的重量数据见附录。
（1）构建这些数据的频数分布表。
（2）绘制频数分布的直方图。
（3）说明数据分布的特征。

2.甲乙两个班各有40名学生，期末统计学考试成绩的分布见附录。
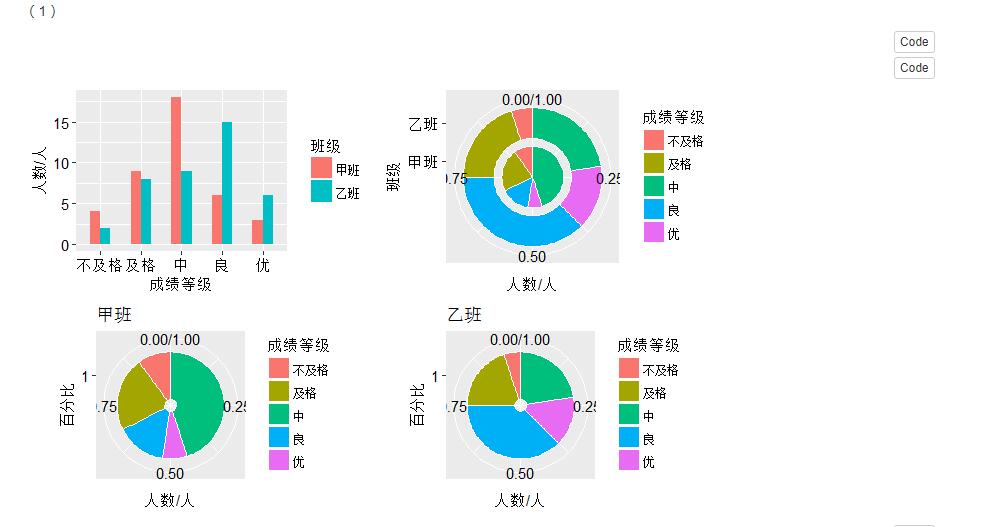
（1）根据上面的数据，画出两个班考试成绩的复合柱形图、环形图和图饼图。
（2）比较两个班考试成绩分布的特点。
（3）画出雷达图，比较两个班考试成绩的分布是否相似。

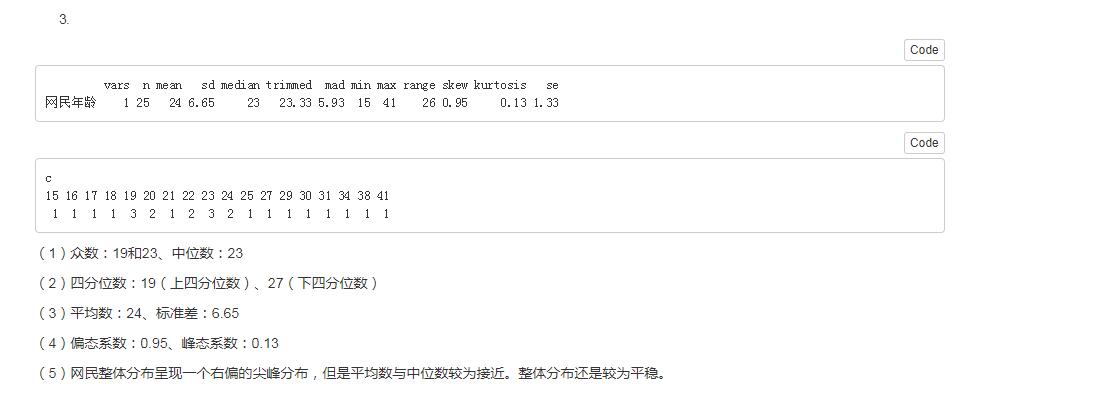
3.随机抽取25个网络用户，得到他们的年龄数据（单位：周岁）见附录。
（1）计算众数、中位数。
（2）根据定义公式计算四分位数。
（3）计算平均数和标准差。
（4）计算偏态系数和峰态系数。
（5）对网民年龄的分布特征进行综合分析。

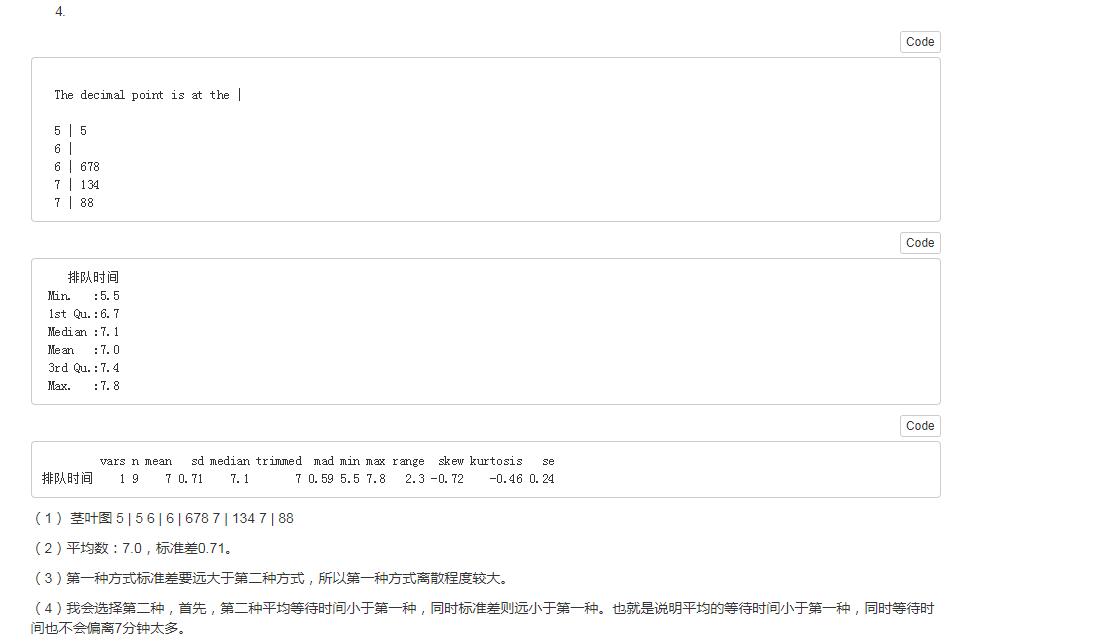
4.某银行为缩短顾客到银行办理业务等待的时间，准备采用两种排队方式进行试验：一种是所有顾客都进入一个等待队列；另一种是顾客在三个业务窗口处列队三排等待。为比较哪种排队方式使顾客等待的时间更短，两种排队方式各随机抽取的9名顾客，得到第一中排队方式的平均等待时间为7.2分钟，标准差为，1.97分钟，第二种排队方式的等待时间（单位：min）见附录。
（１）画出第二种排队方式等待时间的茎叶图。
（２）计算第二种排队方式等待时间的平均数和标准差。
（３）比较两种排队方式等待时间的离散程度。
（４）如果让你选择一种排队方式，你会选择哪一种？试说明理由。

5.从均值为200、标准差为50的总体中，抽取n=100的简单随机样本，用样本均值`x估计总体均值。
a)描述重复抽样的样本均值的抽样分布。
b)不重复抽样，总体单位数分别为10000、1000时的样本均值的抽样分布。

2 参数估计与假设检验

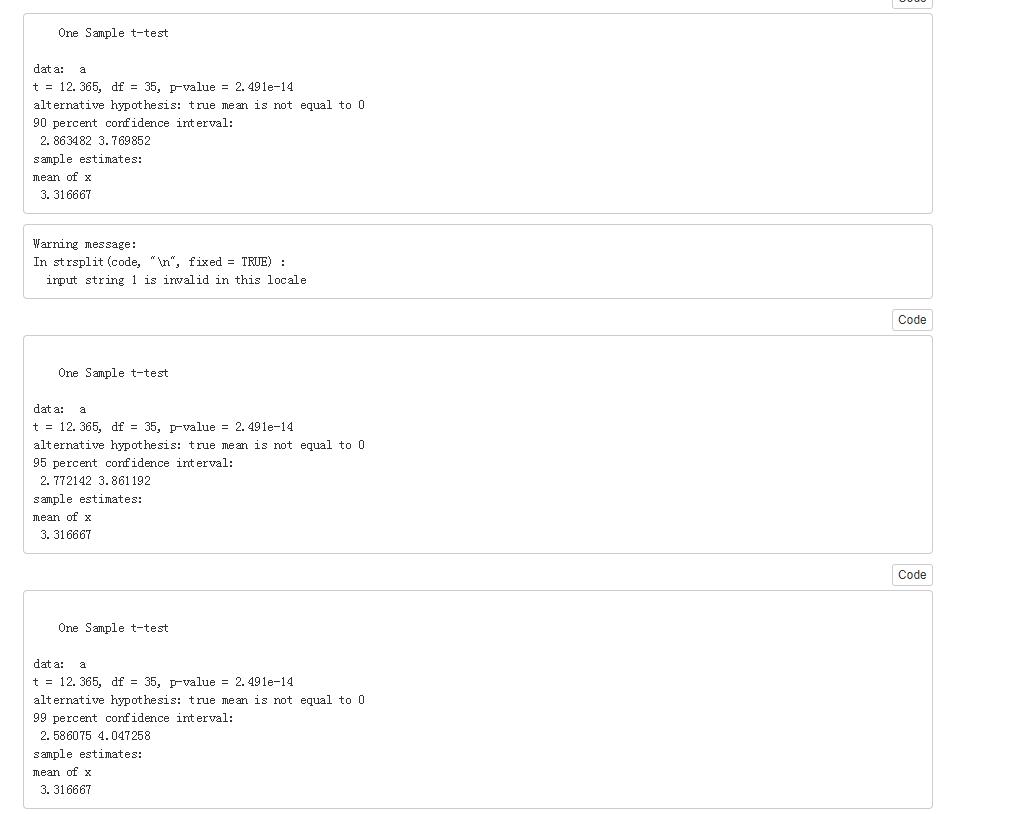
1.某大学为了解学生每天上网的时间，在全校7500名学生中采取不重复抽样方法随机抽取36人，调查他们每天上网的时间（单位：小时） ，得到的数据见附录。求该校大学生平均上网时间的置信区间，置信概率分别为90%、95%和99%。

2.假定两个总体的标准差分别为：=12，=15，若要求误差范围不超过5，相应的置信水平为95%，假定，估计两个总体均值之差时所需的样本容量为多大？

3.经验表明，一个矩形的宽与长之比等于0.618的时候会给人们比较良好的感觉。某工艺品工厂生产的矩形工艺品框架的宽与长要求也按这一比例设计，假定其总体服从正态分布，现随机抽取了20个框架测得比值见附录。在显著性水平 ＝0.05时，能否认为该厂生产的工艺品框架宽与长的平均比例为0.618？。

4.一家大型超市连锁店上个月接到许多消费者投诉某种品牌炸土豆片中60克一袋的那种土豆片的重量不符。店方猜想引起这些投诉的原因是运输过程中沉积在食品袋底部的土豆片碎屑，但为了使顾客们对花钱买到的土豆片感到物有所值，店方仍然决定对来自于一家最大的供应商的下一批袋装炸土豆片的平均重量（克）进行检验，假设陈述如下：

如果有证据可以拒绝原假设，店方就拒收这批炸土豆片并向供应商提出投诉。
（1）与这一假设检验问题相关联的第一类错误是什么？
（2）与这一假设检验问题相关联的第二类错误是什么？
（3）你认为连锁店的顾客们会将哪类错误看得较为严重？而供应商会将哪类错误看得较为严重？

3 方差分析与回归分析

1.某家电制造公司准备购进一批5#电池，现有A、B、C三个电池生产企业愿意供货，为比较它们生产的电池质量，从每个企业各随机抽取5只电池，经试验得其寿命（单位：h）数据见附录。试分析三个企业生产的电池的平均寿命之间有无显著差异（）。如果有差异，用LSD方法检验哪些企业之间有差异？

2.一家超市连锁店的老板进行一项研究，确定超市所在的位置和竞争者的数量对销售额是否有显著影响。获得的月销售额数据（单位：万元）见附录。取显著性水平，检验：
（1）竞争者的数量对销售额是否有显著影响。
（2）超市的位置对销售额是否有显著影响。
（3）竞争者的数量和超市的位置对销售额是否有交互影响。

3.附录中有随机抽取的15家大型商场销售的同类产品的有关数据（单位：元）。
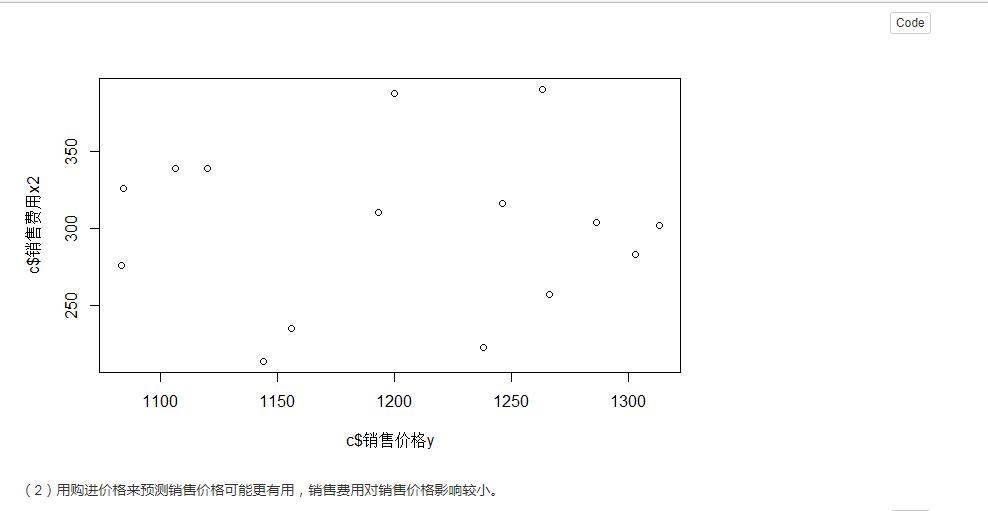
（1）计算y与 、y与之间的相关系数，是否有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系？
（2）根据上述结果，你认为用购进价格和销售费用来预测销售价格是否有用？
（3）用Excel进行回归，并检验模型的线性关系是否显著（）。
（4）解释判定系数，所得结论与问题（2）中是否一致?
（5）计算与之间的相关系数，所得结果意味着什么？
（6）模型中是否存在多重共线性？你对模型有何建议？

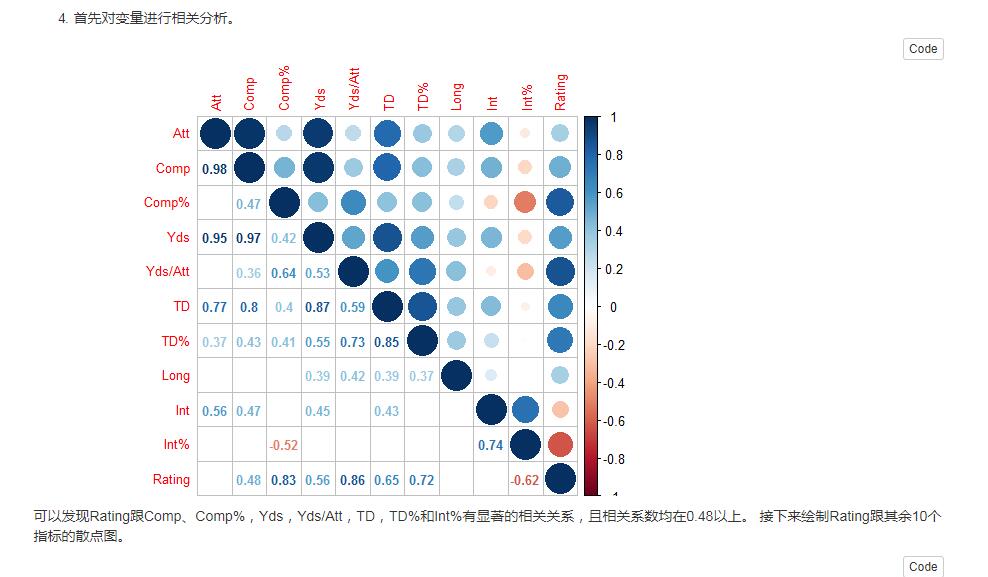
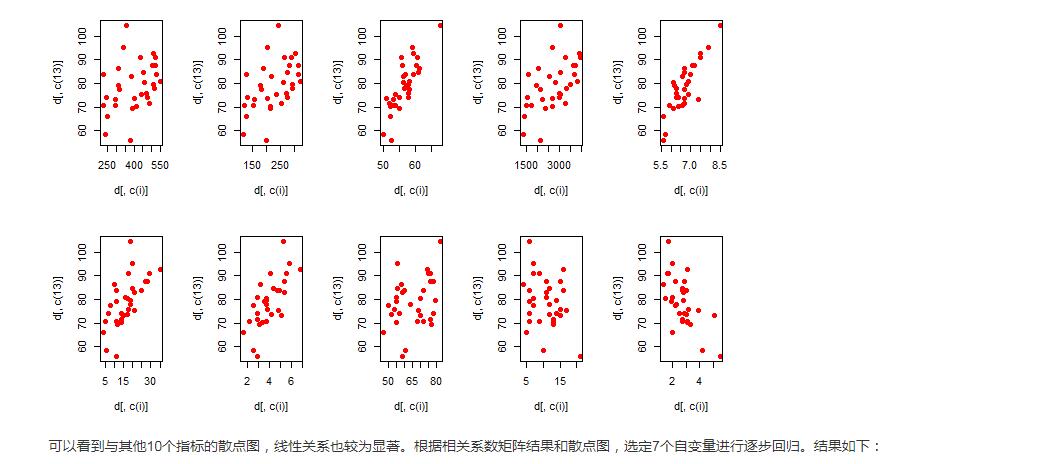
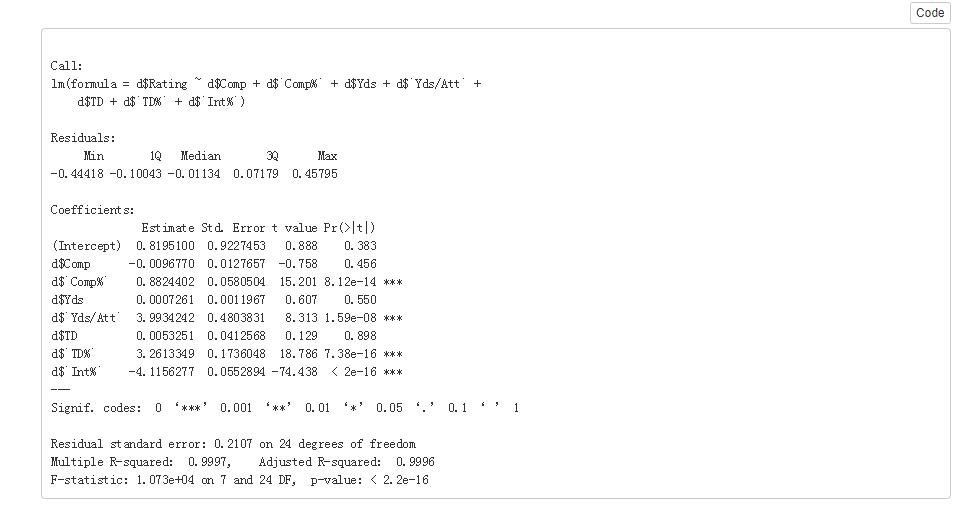
4.附录中有32名美士足球运动员的rating及其他相关信息。请建立一个回归模型以预测一位美士足球运动员的rating。提交报告包括：使用什么方法建立的模型，该方法的运行结果，最终模型的解释（拟合程度、预测误差）。

这一份作业汇总从最原始的描述统计、参数估计、假设检验到基础的方差分析与回归分析均有了。根据这里的习题即可对前面的内容再次熟悉。
这里就不多说了，我有一份比较完整的文档针对这份内容。这里先给出节选部分的截图。具体地址再给出。